선형대수학 5.1


예제1) 에서 볼 수 있듯, 벡터 v에 Linear Transforamtion을 시행했을 때 Av 가 기존의 벡터 v의 상수배 한 것으로 표현이 되는 순간이 존재한다.

이처럼 벡터의 Transformation by Matrix를 시행했을 경우 기존의 백터의 상수배로 표현이 된다면 시그마(T) 를 eigenvalue라고 하고
이를 만족하는 벡터 x를 eigenvector라고 한다.

Ex2) 에서는 각각 벡터 u와 v가 eigenvector인지를 묻는 문제이고 각각, Au, Av를 시행해서 Transformation된 벡터가
기존 백터의 상수배로 표현이 가능하다면 해당 벡터는 Matrix A의 eigenvector라고 할 수 있는 것이다.

Ex3) 은 숫자 7이 Matrix A의 eigenvalue인지를 묻는 문제이다.

우선 Eigenvector처럼 표현될 수 있음을 가정하고 (1) 처럼 서술할 수 있다.

그리고 (2) 식을 Homogeneous Equation의 각각의 column들이 Linear Dependence 한지를 검사하면 된다. Ax의 x와 7x의 x는
서로 상수배에 해당하는 벡터일 것이므로 선형 종속일 경우 7이 eigenvalue가 되는 것을 확인 할 수 있다.

정리 1

요약하면 (3)번 식처럼 표현이 되고 Homogeneous 식이 nontrivial solution을 가질 경우 (선형 종속인 경우) 해당 set을 eigenspace 라고 부른다.
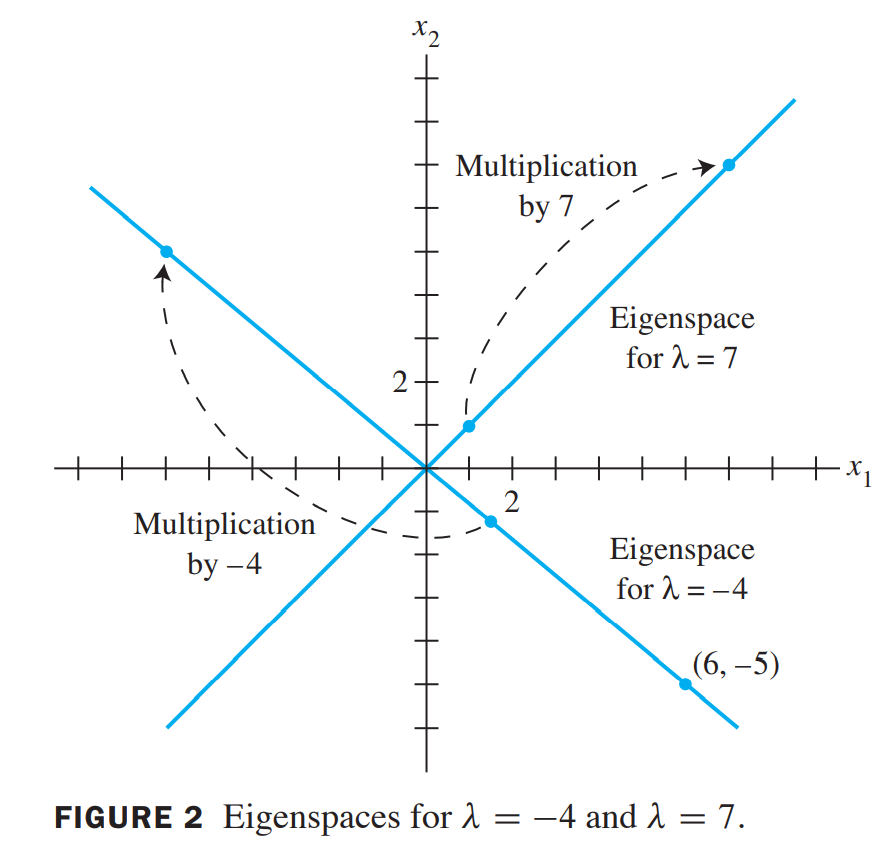
시그마(T), Eigenvalue 가 7인 경우는 벡터 (1,1)의 상수배에 해당하는 x2 = x1의 직선이 Eigenspace가 된다.

Ex4)는 Matrix A의 eigenvalue가 2일 때 Basis를 찾는 문제이다.
이 경우 eigenvector의 Homogeneous Equation 을 작성하고 Linear Dependence한 다시 말해서 free variable을 가지는 변수로
Parameter vector form을 형성하면 Basis를 구성하는 columnn 벡터를 구할 수 있을 것이다.

우선 Homogeneous Equation을 작성하고 free varaible에 대한 식으로 표현을 한다.


최종적으로 원점을 지나는 하나의 평면이 Eigenspace이고 이에 해당하는 Basis는 위와 같을 것이다.
정리 2

즉, Upper Triangle 혹은 Lower Triangle로 표현된 Matrix의 경우 EigenValue를 바로 찾을 수 있는 데 이는 Main diagonal에 있는 수가
바로 eigenvalue가 된다는 것이다.
정리 3

column 벡터가 r 개 있는 Matrix에서 eigenvalue가 모두 distinct 하다면 v1 ~ vr 로 이루어지 집합은 선형 독립이라는 정리.