
Graph Exploration
Vertex에 가서 무엇인가 일을 하는 Count, number 하는 것을 Visit이라고 한다. BFS와 DFS 두 가지 방법이 있다. Connected Component가 무엇인지를 찾아내야 한다. Vertex와 node 들이 다 연결 안될 수 도 있다. 독립된 Component를 판단할 수 있어야 한다. Spanning tree를 계산하는 것도 다시 공부해볼 것이다.

BFS
Tree 안에는 기본적으로 모든 Vertex가 포함되어야 한다. 모든 Edge는 포함되지 않을 수도 있다. Explored edge는 추후에 더 알아보기로 함. One vertex at a time, Serial 모드에서 다루기 때문에 한 번의 Vertex를 다룬다. 임의의 vertex를 사용하는 데 시작을 Source vertex라고 부른다. Root로 시작을 하면 child가 계속 생기게 된다. Tree가 만들어지고 Source부터 node까지 shortest path는 tree에 있는 Path가 된다. Discover the vertex는 vertex를 처음 만났을 때를 말하고 Explore도 마찬가지 이다.

BFS
3개의 color를 가지고 있다고 가정을 할 것이다. Discover 되지 않는 vertex를 white라고 한다. Gray 색은 방문 중이라고 할 수 있다. W->G->B 순서로 진행하게 된다.

BFS
White가 발견되면 Gray로 변하게 되고 연결된 모든 White를 Discover 하게 된다. 이후 모든 이웃을 Discover하면 비로소 Black으로 바꾸게 된다. Gray가 된 순간 adjacency list로 포함 시킨다.

BFS
BFS의 수도 코드. 첫 부분은 Initialize하는 것이다. 초기화는 무한대로 해놓고 Parent가 누구인지 지정하는 것이 파이 배열이라고 초기화 시킨다. source vertex의 색을 Gray로 바꾸고 Parent는 없고 distance는 0이다. Q에 있는 vertex를 하나 꺼내고 자기와 연결된 White를 발견하면 GRAY로 바꾸고 Distance를 하나 증가시키면서 Parent를 자기 자신으로 설정하게 된다. 끝나게 되면 자기자신을 Black으로 바꾸게 된다.

Analysis
Running time을 얘기하는 것이 중요하다. while과 for 둘 다 존재하기에 측정하기 어렵다. 모든 node는 한 번 Queue에 들어가게 된다. 모든 Node들이 Queue에서 한 번 나오게 되고 adjacency list이 한 번 scan이 된다. 총 running time은 세타 V+E가 된다. 기본적으로 모든 노드를 한 번 검사를 하고 방문을 해야 하므로 이것보다 빠르게 할 수는 없다. Running time이 이보다 빠를 수는 없게 된다. DFS와 BFS모두 마찬가지 이다.
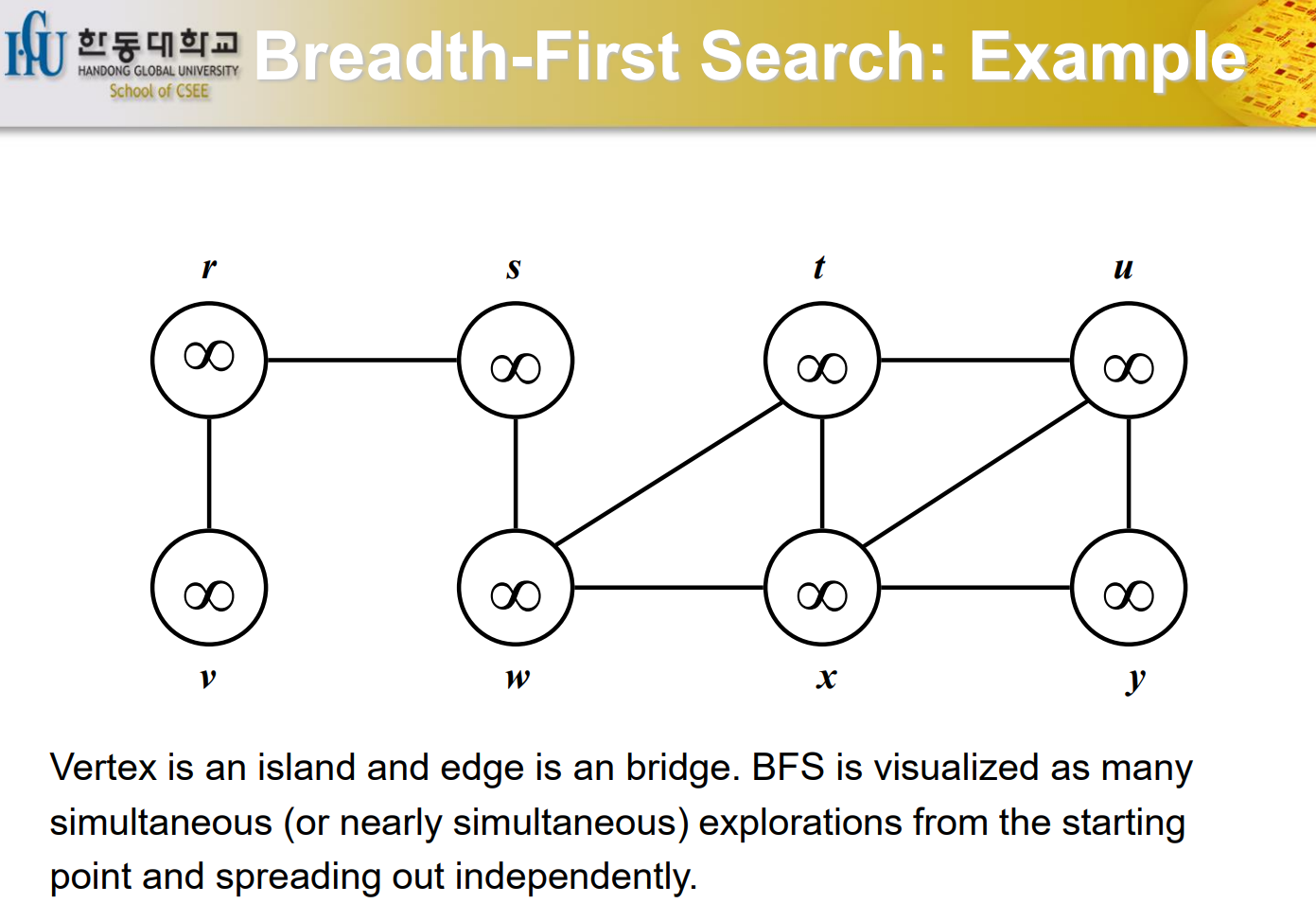
BFS Example
Distance를 모두 무한대로 초기화를 한다. Vertex가 섬이고 edge는 이어주는 다리라고 생각하면 쉽다. BFS는 s node에서 시작을 한다. 사람들이 r 섬과 w 섬은 거의 동시에 발견이 된다. r, t, x섬은 또 동시에 발견되기도 하고 그렇게 된다. Q에는 s Node를 넣게 된다. Q가 empty가 아닌 동안 반복을 하게 되는데 s와 연결된 Node를 계속 검사하게 된다. 색깔을 Gray로 바꾸고 끝나게 되면 S node를 Black으로 바꾸게 된다. w를 먼저 넣었으므로 t와 x node를 Gray로 먼저 바꾸게 되고 다 끝나면 w를 Black으로 바꾸게 된다. 다음으로 r의 인점한 v가 Gray가 되고 r은 Black이 된다. BFS tree가 만들어지게 된다. parent를 기억하게 되고 child가 계속 만들어지게 된다. 모든 Vertex가 포함이 되고 edge들은 graph의 모든 edge가 포함되지 않을 수도 있다는 점이 특징이다.
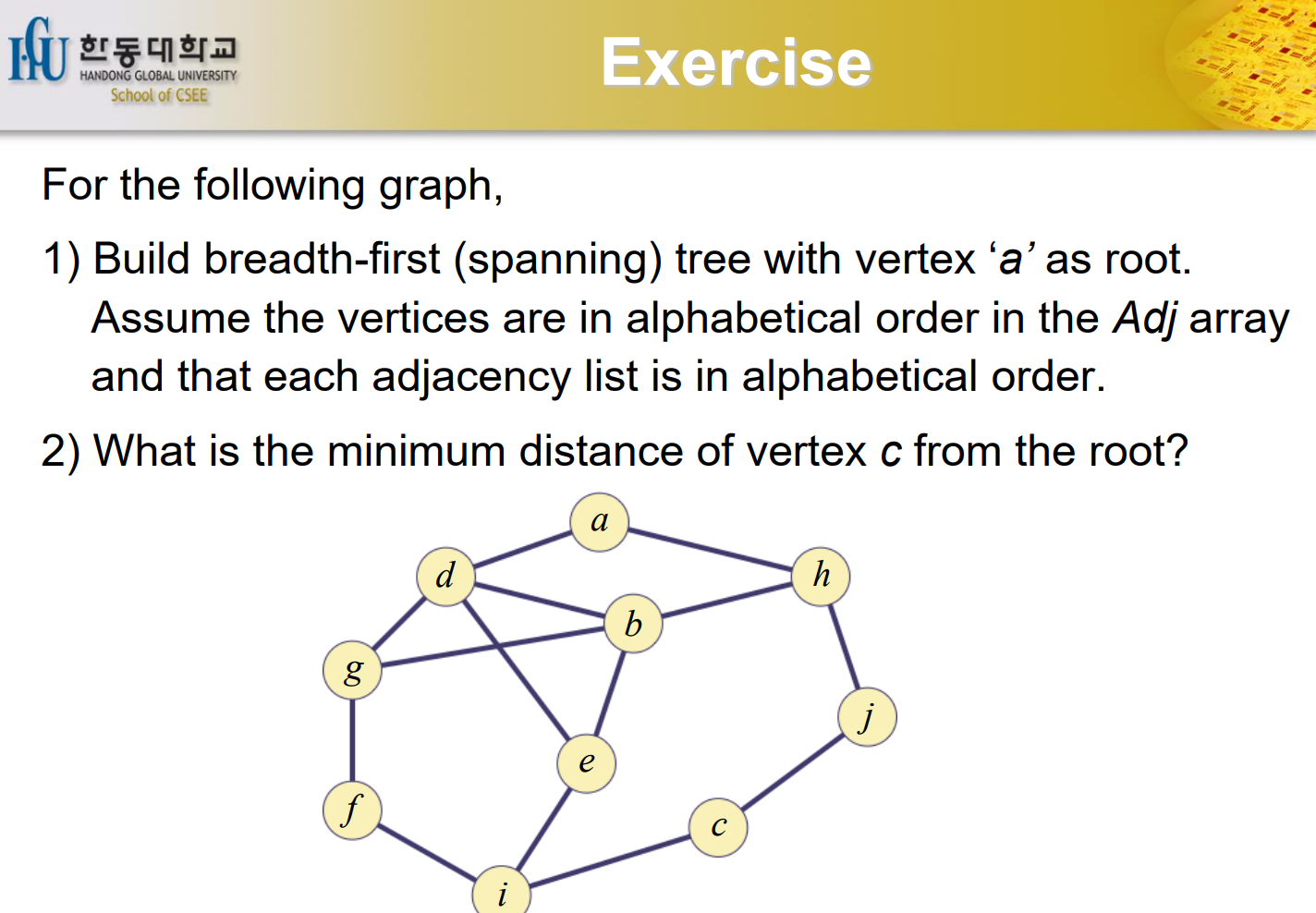
Exercise
a를 Root로 하는 order의 배열이 있는 경우 어느 노드를 먼저 가야 할까. adjaceny list를 만들때 alphabet order로 node가 들어가게 된다. a에서 c까지의 distance는 3이 된다. c의 parent는 j가 된다.
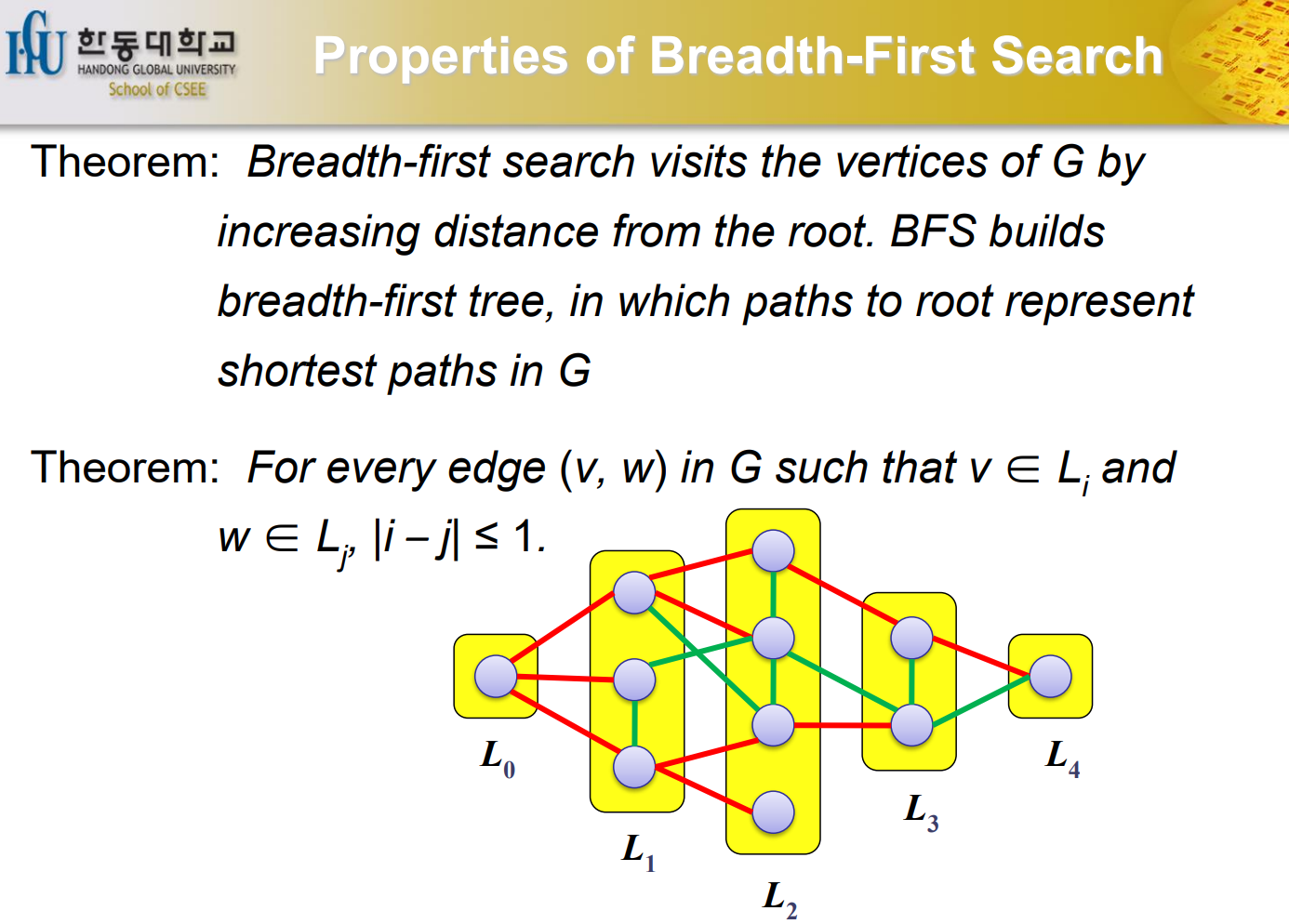
Properties of BFS
distance가 2 이상 날 수 없다는 것. 너무 당연하다.
-------------

DFS
Explore라는 것은 모든 Vertex를 방문하는 것을 얘기한다. 가능한한 깊게 밑으로 들어가려는 것이다.
S 가 root node가 된다. 가장 recently 발견된 node에서 계속 깊게 들어간다. 다 explore할 수 없으면 back tracking을 하게 된다. explore 되지 않은 vertex가 있으면 discover하게 된다. 연결된 독립된 Graph가 있었다고 하면 Traverse안된 graph도 Explore해야 한다.

DFS
BFS 경우 source가 있고 adjaceny list에 알파벳 순서로 들어가게 되는데, DFS는 그렇지 않다. Source가 있고 a가 연결되었다면 a와 연결된 것을 계속 탐색해 나간다. 이미 발견된 vertex와 연결된 edge는 check 되었다고 표현한다.

DFS
각각의 노드 마다 discovery time과 finish time이 있다. V개의 node가 있으면 두 개의 time 이 존재한다. 모든 노드의 color를 White로 초기화를 한다. global 변수로 time이 필요하다. 그리고 각각의 node에 대해서 WHite이라면 DFS_Visit function call을 하게 된다. DFS VISIT을 한 번 call 할때마다 tree가 생긴다.
DFS Visit
Gray로 색을 바꾸게 되고 time 전역 변수를 증가시키게 된다. 연결된 모든 node에 대해서 recursive하게 call을 한다. a와 연결된 모든 node를 방문하고 나면 Black으로 바꾸고 time을 증가해서 finish time stamp에 넣게 된다. BFS에서는 Queue를 사용하고 DFS에서는 Stack을 사용할 수 있다. Back Track이라는 말이
나왔었다. Back track을 할 때는 Stack 데이터 구조를 사용하게 된다. 하지만 Stack을 사용하지 않고 Recursion을 사용했다. activation 이 올라가고 stack으로 만들기 때문에 기본적으로 stack을 사용하는 것과 마찬가지의 효과를 내게 된다. discover time과 finish time을 계산하게 된다.

DFS Example
Direct Graph라고 생각해보자. DFS는 한 사람이 건너간다고 생각해야 한다. d = 1로 source가 시작을 하고 Visit을 진행해야 한다. 건너가서 2인 vertex를 발견하고 건너가면 edge가 검은색으로 표시된다. 더 이상 갈 곳이 없으면 discover time과 finish time을 설정하게 된다. 방문하지 못한 vertex에 대해서 다시 DFS_VISTIT을 call하게 된다.

Analysis DFS
DFS(G)는 각각 vertex의 개수만큼 필요하게 된다.
--------------
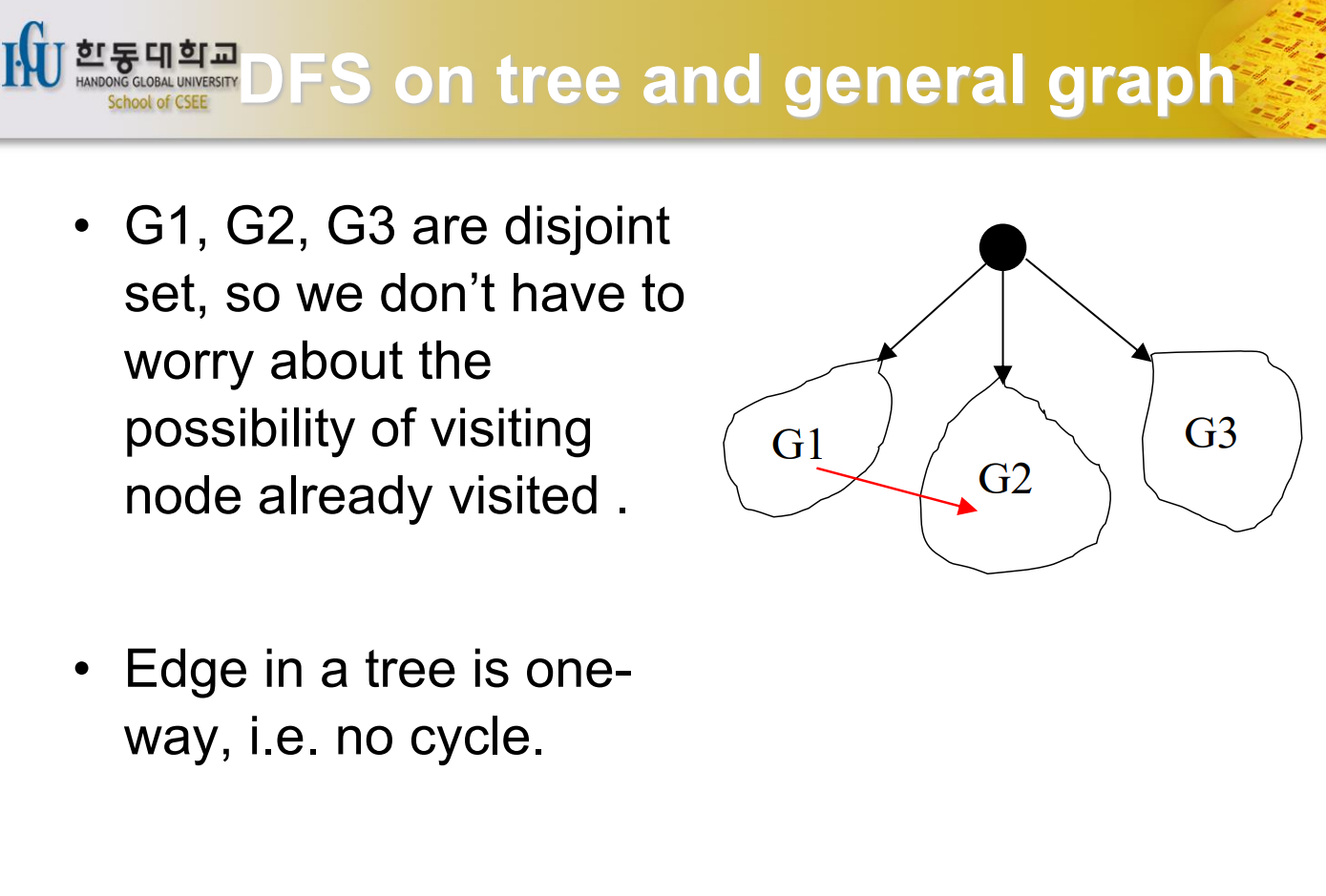
DFS on tree and general graph
Tree인 경우와 Tree가 아닌 경우에 차이점이 존재한다. cycle이 없으면 tree라고 할 수 있다. Vertex가 N이고 Edge가 N-1이고 Cycle이 없으면 Tree라고 할 수 있다.
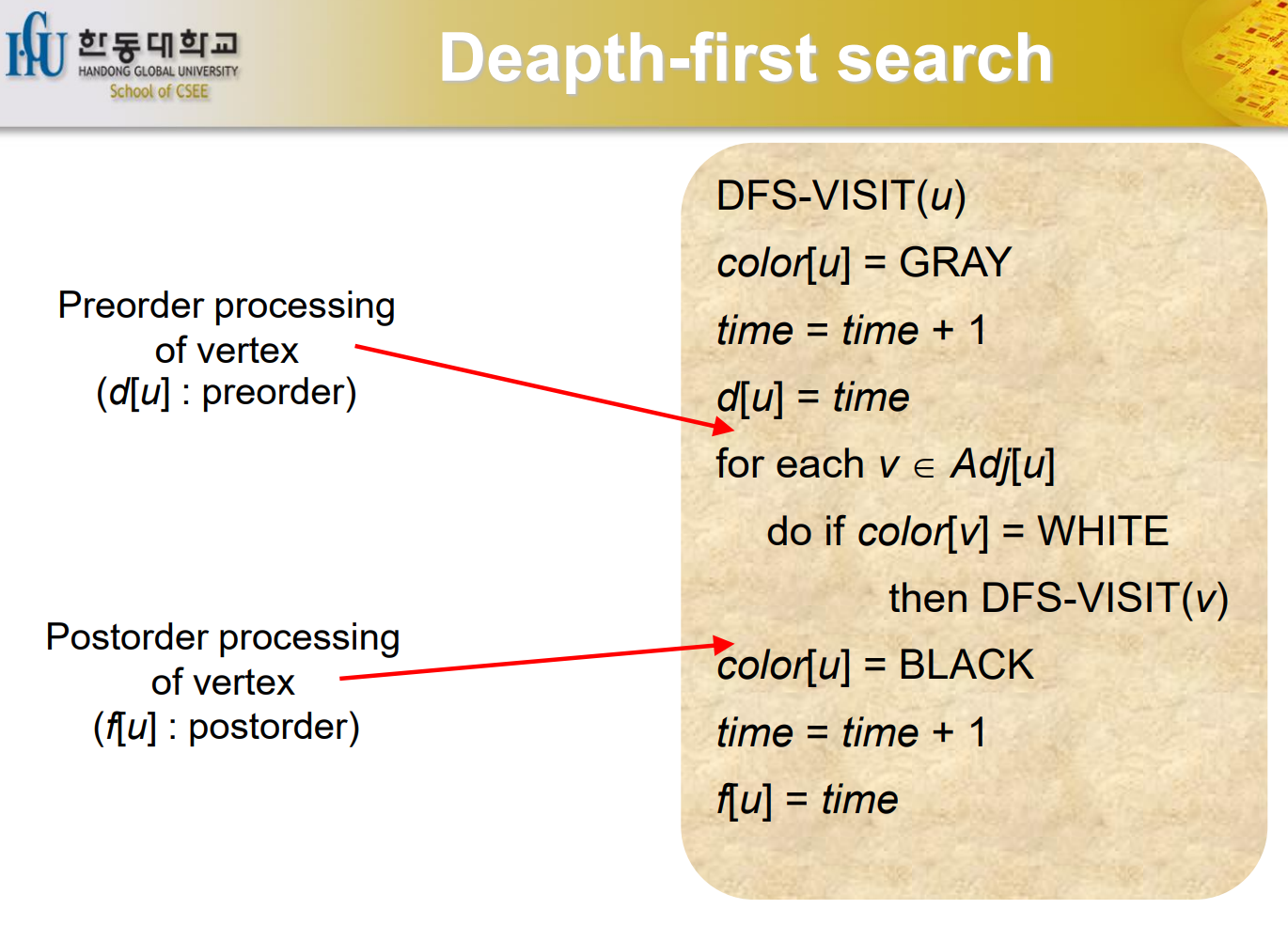
DFS
Binary Tree라고 배웠을 것이다. Inorder, Preorder, PostOrder.... preorder 는 방문하기 전에 무언가를 할때를 말하고 post order는 visit을 한 이후에 무엇인가를 한 경우를 말한다. inorder는 DFS에서 쓰이지 않는다.
DFS
방문을 했을 때 True라고 하고 방문하지 않는 vertex이면 call하는 것을 코드로 나타낸 것이다.

Parenthesis theorem
1번, 2번, 3번의 경우 중 하나이지 다른 경우로 존재할 수는 없다. 이것이 parenthesis theorem이다. u라는 노드가 있고 v라는 연결된 노드가 있다고 하자. U를 먼저 discover하고 v를 discover하고 v가 finish 되고 u가 finish 되는 순서를 따른다. 2번은 U와 V가 이동할 수 없는 graph인 경우를 의미한다. 마치 괄호와 같다해서 이름이 붙여졌다. Corollary라는 것은 v가 u의 후손인 경우 u가 v 밖에 존재하는 괄호라고 알 수 있다.
Parenthesis theorem
Parenthesis theorem
Parenthesis theorem
Parenthesis theorem

DFS: Kinds of edge
Tree edge라는 것이 있다. 어떤 노드에서 다음 노드를 만났을 때 Gray라는 상태에서 White를 만났을 때 Tree edge로 만들어지게 된다. 이런 것을 Tree edge라고 한다. forest라고 하는 것은 tree가 여러 개 있을 때이므로 그렇게 부른다. cycle이 이루어질 수는 없다.
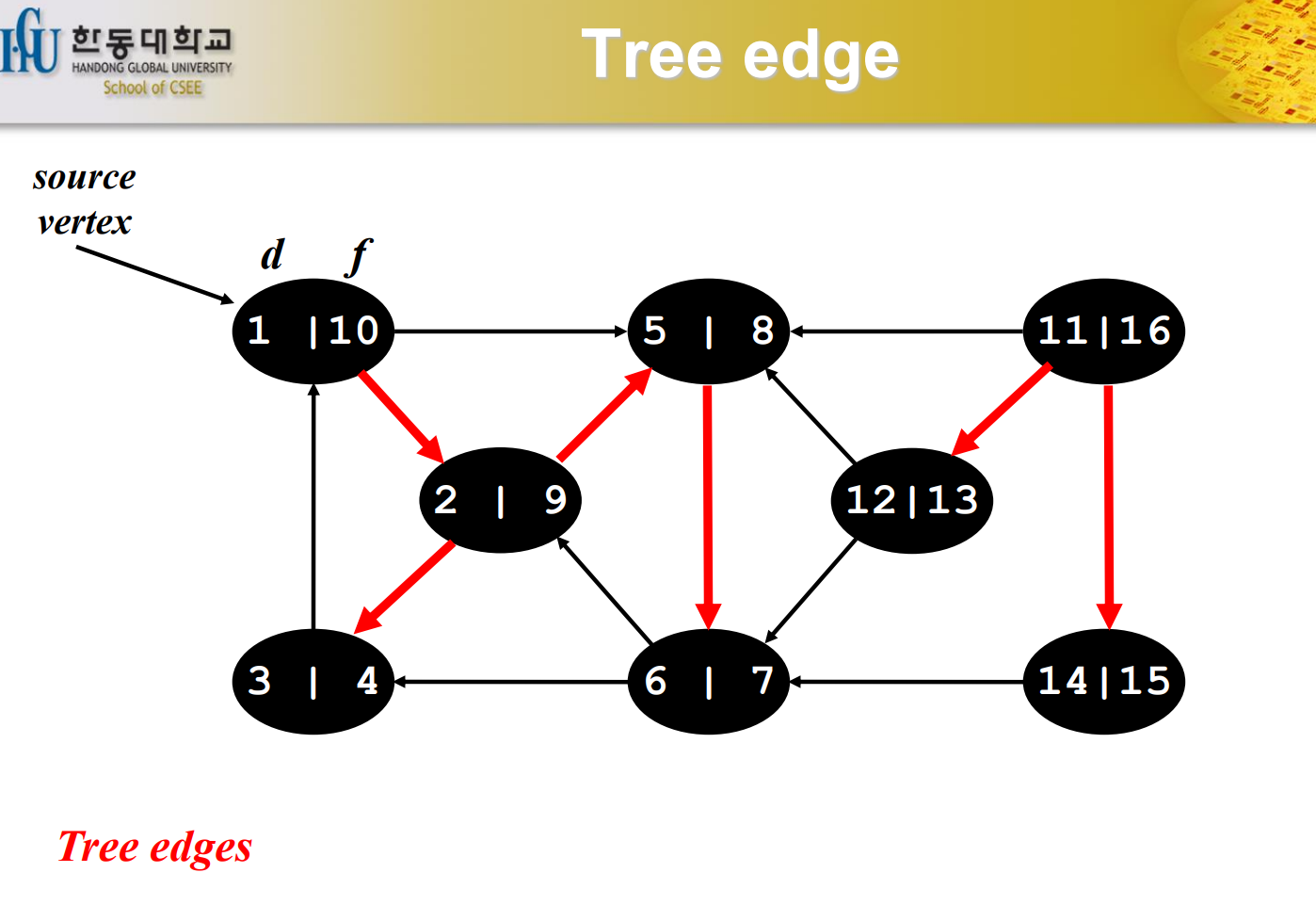
Tree edge
다리를 건너갔다고 표현한 빨간색 edge가 tree edge가 된다. 지나간 다리에 해당한다.

DFS Kinds of edge
Back edge는 Gray에서 Gray로 갈때 Back Edge가 된다. descendent로 부터 ancestor로 가는 edge를 말하게 된다.

DFS Kinds of edge
Forward edge는 Gray로부터 Black으로 가는 경우를 의미한다. 초록색에 해당한다.

DFS Kinds of edge
Cross edge라는 것은 Tree가 있는데 서로 다른 Tree가 존재할 수 있다. Tree와 Tree 사이의 Edge를 cross edge라고 한다. Gray에서 Black으로 가는 경우를 말한다. 보라색이 Cross edge가 된다.
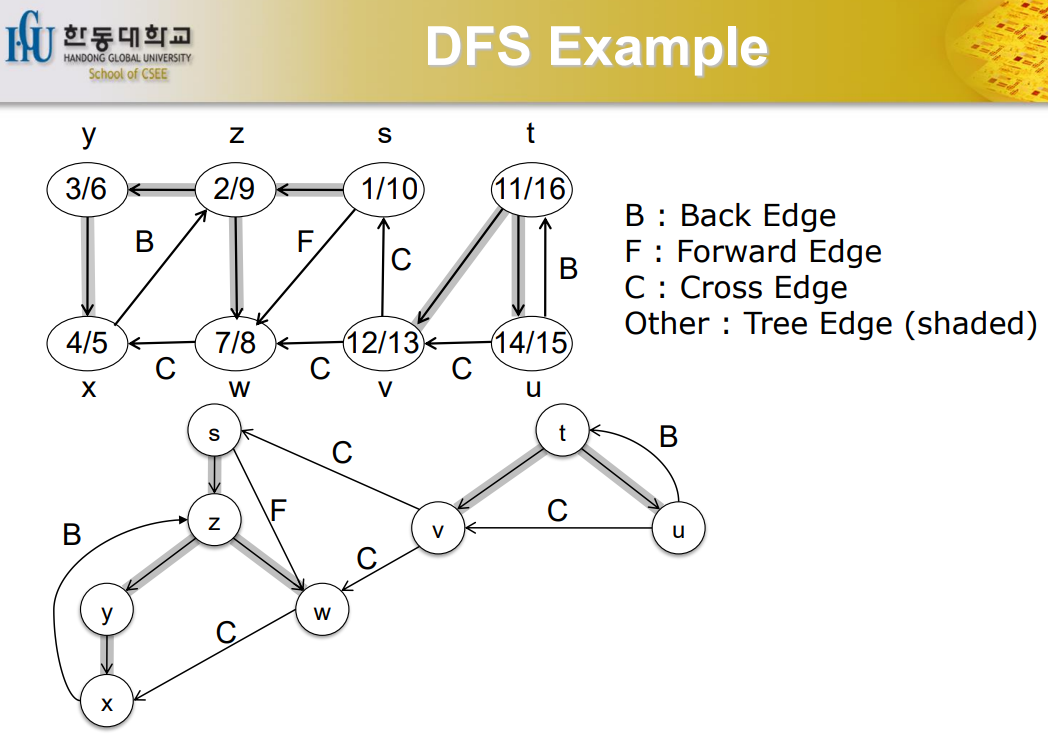
DFS Example
알파벳 순서로 하게 된다. edge에 대한 구분도 적혀있으니 스스로 공부해볼 것.

DFS Kinds of edge
discovery time과 finish time을 가지고 확인을 하면 구분할 수 있다.

DFS on Undirected graph
BFS를 할 때 사용한 방법을 사용한다. 먼저 방문해서 edge를 살펴볼 필요가 있으면 자연스럽게 방향을 설정했던 느낌을 사용한다. 어느 방향으로 방문을 할지를 선택하게 된다.

DFS Kinds of Edges
G가 undirected graph 라고 했을 때 tree edge와 back edge만 나올 수 있다. Forward edge는 방향을 가질 수 없다.
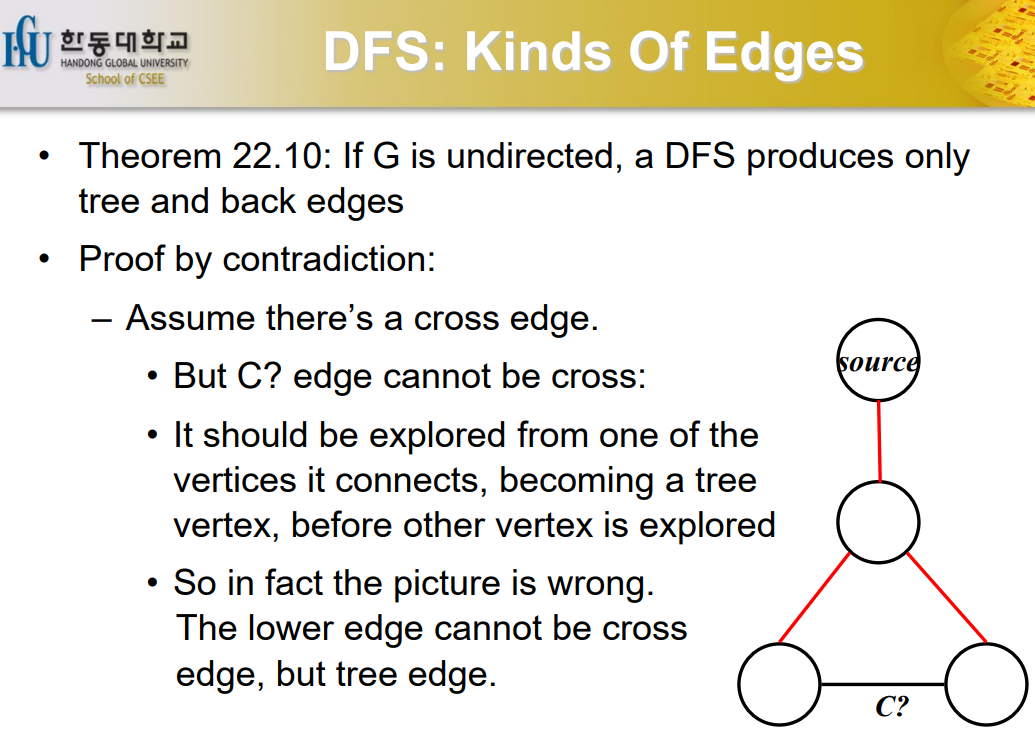
DFS Kinds of Edges
cross edge가 절대 나올 수 없다.

DFS vs BFS
DFS는 recursion을 사용하므로써 Stack의 논리를 따른다고 해도 무방하다.
DFS는 2개의 방법이 존재한다. 처음 발견되었을 때 Processing을 하는 것이 Preorder가 된다. 끝났을 때 하는 것을 Postorder Processing 이라고 한다. (*********) 강의 다시 들어서 이해하기

Topological Sort
DAG라는 것. Directed이다. 방향성이 존재한다.

Topological Sort Algorithm
finish time을 만들고 decreasing 하는 것을 의미한다.

Getting Dressed Example
Watch라는 것은 언제 차도 상관없다. Shirt부터 해서 Tie를 매고 등등으로 방향을 잡아간다. 임의로 watch를 선택함.
finish time이 큰 것 먼저 정렬을 하게 된다.

Topological Sort Algorithm
DFS Search는 V+E 만큼 시간이 걸린다. Correctness를 어떻게 검증할까 u에서 v로 가는 경우 finsih time은 u가 더 크다고 할 수 있다.

Correctness of Topological Sort
U에서 V로 가는 경우, U는 Gray이고 v가 Gray일 때 이는 모순이다. Cycle이 존재할 수 없다.
V가 White인 경우, finsih time이 u가 v보다 크게 된다. V가 Black인 경우, Forward Edge인 경우 V는 이미 끝나있다.

Connected Component
undirect graph에서 일어나는 일이다. DFS 함수, DFS-VISIT을 call하기 전에 label을 만들어서 call을 하게 된다.
DFS-VISIT은 그 라벨을 받아서 패스하게 된다..
Depth-first search
DFS_VISIT 호출 전에 id를 파라미터로 넘기면 해당 id를 가진 Connected Graph를 구분할 수 있게 된다.

Strongly Connected Component
directed graph에서 일어나는 일이다. maximal이라는 것은 모든 vertex에서 다른 곳으로 갈 수 있어야 한다. u에서 v도 있고 v에서 u도 있어야 한다.
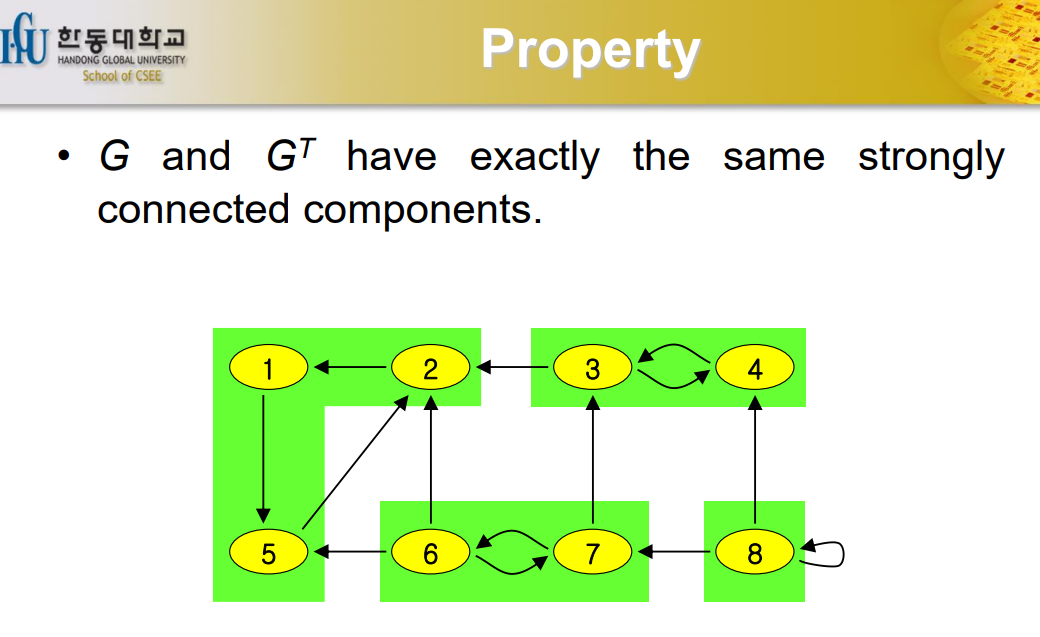
Property
Strongly connected component는 transpose를 하더라도 동일한 성질을 가진다. 그리고 그 component를 하나의 노드로 생각을 하게 되면 그 그래프는 DAG를 만족한다. direction도 있고 cycle이 존재하지 않는다.

Algorithm
1번에서는 DFS를 실시한다. 2번에서는 transpose를 하고 3번에는 finish time이 큰 node부터 시작을 하게 된다. 이렇게 하면 Strongly Connected Component를 구할 수 있게 된다. Tree가 하나씩 나오게 되는데 그 Tree 하나가 Strongly Connected Component에 해당한다.
1번은 세터 V+E 만큼 걸린다. 2번은 v^2만큼 봐야 하지만 Linked List가 있다면 세타 V+E만큼 걸린다고 할 수 있다. 3번에서 DFS를 call하므로 동일한 시간이 걸리고 4번은 Constant 만큼 걸린다고 할 수 있다. 굉장히 빠른 알고리즘이라고 할 수 있다.

G vs transpose
Finish time of SCC를 정의해야 한다. 1번 노드에서 시작을 해서 2번으로 갔다고 하자. 3,4 -> 6,8까지 가면 8의 finish time이 제일 빠르게 된다. 6,7 노드의 finish time이 2번째가 되고 3,4번에 3번째 1,2,5가 4번째가 된다. finish time이 제일 큰 1,2,5 중에서 Transpose의 DFS가 시작되는 것이다.

Step1.
Step3
Transpose의 DFS가 끝나서 Back track을 하게 되는 것이 하나의 Strongly Connected Component가 된다.

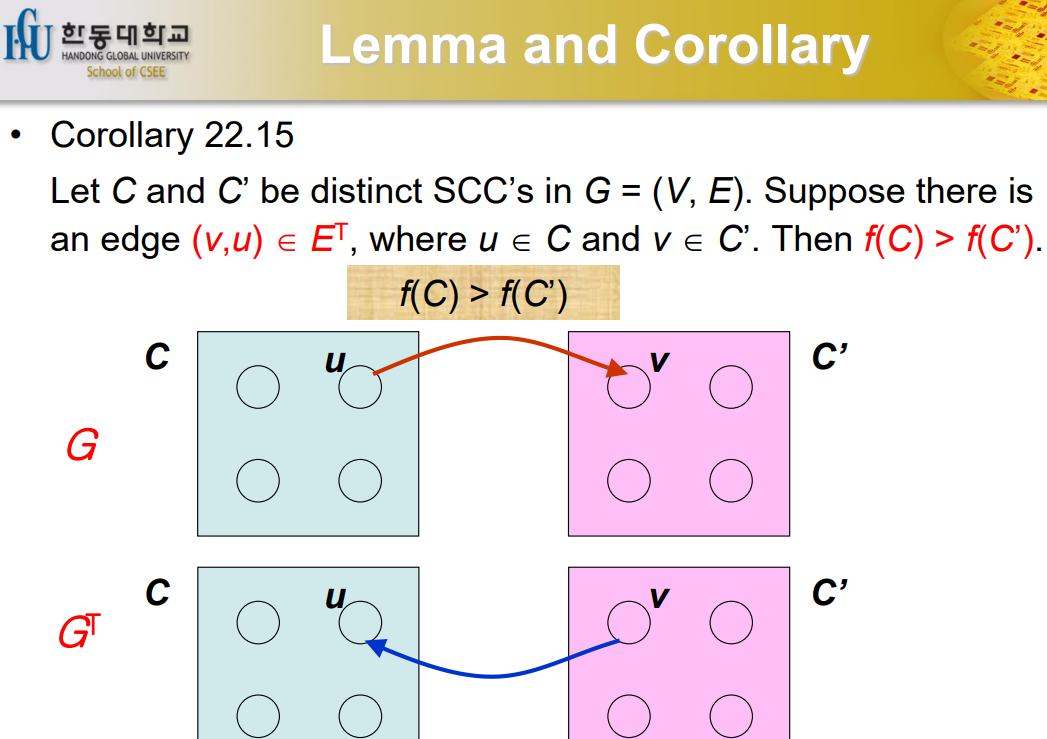
Lemma
C에서 C'으로 가는 edge가 있다면 그 반대는 있을 수 없다는 것이다.

Lemma and Corollary
Vertex의 finish time을 계산하고 가장 큰 애 가장 늦게 끝나는 애. u에서 v로 가는 edge가 있다고 하면 finish 되지 않은 상태에서 C'으로 넘어간 경우 C'이 먼저 끝나게 된다. 다시 Back track을 하게 되고 C가 끝나게 된다. 그러므로 C의 finish time이 C'의 finish time보다 클 수 밖에 없다.
Lemma and Corollary
C에서 C'으로 갈 수 있다고 하면
'🚗 Major Study (Bachelor) > 🟨 Algorithm' 카테고리의 다른 글
| 알고리즘 11주차 목요일 (0) | 2022.05.12 |
|---|---|
| 알고리즘 9주차 목요일 (0) | 2022.04.28 |
| 알고리즘 7주차 목요일 (0) | 2022.04.14 |
| 알고리즘 7주차 월요일 (0) | 2022.04.08 |
| 알고리즘 6주차 목요일 (0) | 2022.04.07 |



